Jump to heading🔗 Module 7–01 Rectangular Coordinate System

Jump to heading🔗 1.Coordinate Relationships Between Two Points

• Points on the coordinate axis don't belong to any quadrant.
  • Points on x-axis $(x,0)$.
  • Points on y-axis $(0,y)$.

Jump to heading🔗 2.Coordinates of the Midpoint Between Two Points

• The coordinates of the midpoint between two points $p_1(x_1,y_1)$ and $p_2(x_2,y_2)$ are $(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\boxed{{\displaystyle \text{Average}}}$.
  • Special case: The midpoint between point $p_1(x_1,y_1)$ and the origin $(0,0)$ is $(\frac{x_1}{2},\frac{y_1}{2})$.
  • Formula derivations

    $\begin{array}{l}{x}_2-x=x-x_1\\ x=\frac{x_1+x_2}{2}\\ y=\frac{y_1+y_2}{2}\\ p_1+p_2=2p\\ p=\frac{p_1+p_2}{2}\end{array}$

Jump to heading🔗 3.Distance Formula Between Two Points

• The distance between two points $A(x_1,y_1)$ and $B(x_2,y_2)$ is $d=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}$.
• Special case: The distance between point $A(x,y)$ and the origin $(0,0)$ is $d=\sqrt{x^2+y^2}$.
• Formula derivations

  $\begin{array}{ll}{c}^2=a^2+b^2\Rightarrow c=\sqrt{a^2+b^2}& \text{Pythagorean theorem}\\ AB=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}\end{array}$

Jump to heading🔗 4.Focus 1

Midpoint formula

• Analyze using the midpoint formula $(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})$.

Jump to heading🔗 Solution

Jump to heading🔗 Conclusion

• Derived Solution

  $\mathbf{(}\mathbf{A}\mathbf{)}$
  According to the Solution, get $\{\begin{array}{l}x=4\\ y=-3\end{array}$, so choose $A$.

• Formula used

  $\begin{array}{ll}(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})& \text{Midpoint formula}\end{array}$

Jump to heading🔗 5.Focus 2

Distance formula

• Analyze using the distance formula $d=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}$.

Jump to heading🔗 Solution

Jump to heading🔗 Conclusion

• Derived Solution

  $\mathbf{(}\mathbf{D}\mathbf{)}$
  According to the Solution, get $x=8\vee x=-4$, so choose $D$.

• Formula used

  $\begin{array}{ll}d=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}& \text{Two-point distance formula}\\ x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}& \text{Quadratic formula}\\ \{\begin{array}{l}(a+b{)}^2=a^2+2ab+b^2\\ (a-b{)}^2=a^2-2ab+b^2\end{array}& \text{Perfect square formula}\end{array}$

Jump to heading🔗 Solution

Jump to heading🔗 Conclusion

• Derived Solution

  $\mathbf{(}\mathbf{D}\mathbf{)}$
  According to the Solution, get $\sqrt{(x-2{)}^2+y^2}=\sqrt{(x-5{)}^2+(y-3\sqrt{3}{)}^2}=6$, so choose $D$.

• Formula used

  $\begin{array}{ll}d=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}& \text{Two-point distance formula}\end{array}$

• Additionally, if the problem is an isosceles right triangle

  $\begin{array}{l}\text{Isosceles right triangle: }AC=BC=\sqrt{2}AB⟹AB=\sqrt{2}AC=\sqrt{2}BC\\ \text{Let }C=(x,y)\\ \sqrt{3^2+(3\sqrt{3}{)}^2}=\sqrt{2}\times \sqrt{(x-2{)}^2+y^2}=\sqrt{2}\times \sqrt{(x-5{)}^2+(y-3\sqrt{3}{)}^2}\\ \text{After that, directly substitute the options.}\end{array}$

Jump to heading🔗 Module 7–02 Straight Line

Jump to heading🔗 1.Angle of Inclination

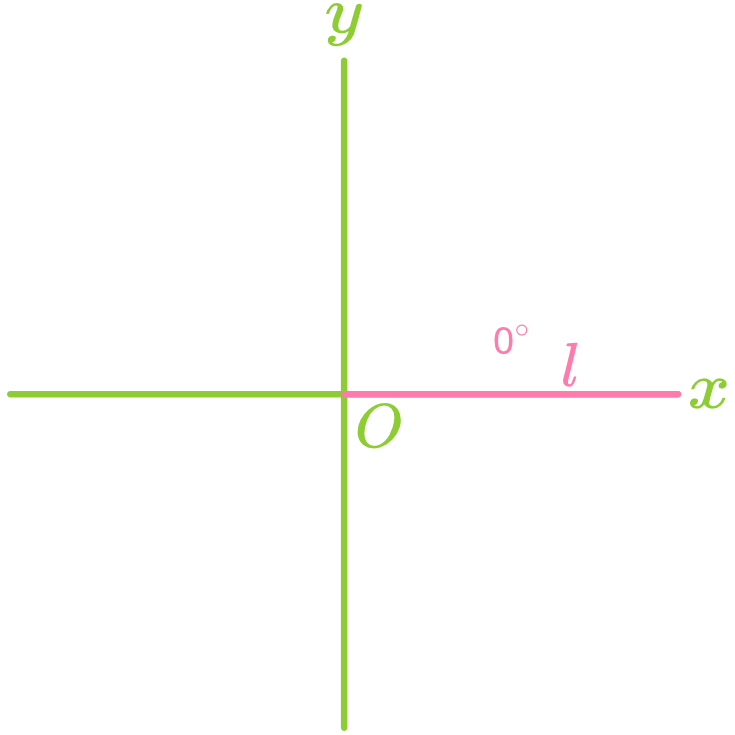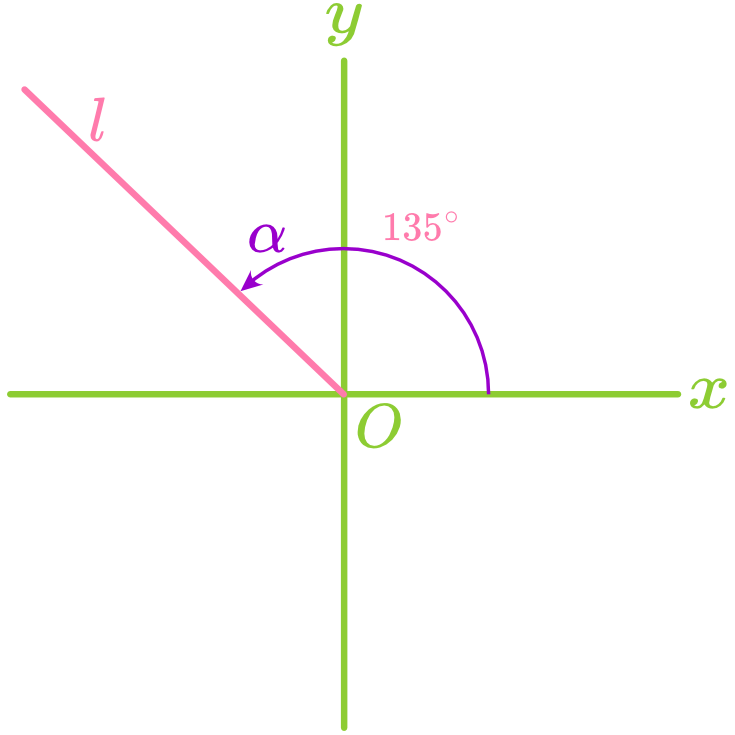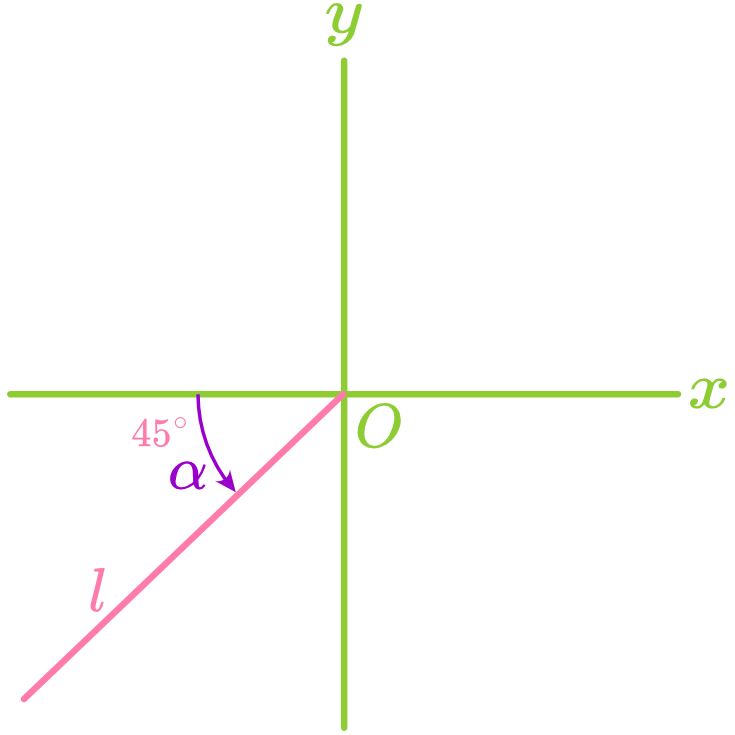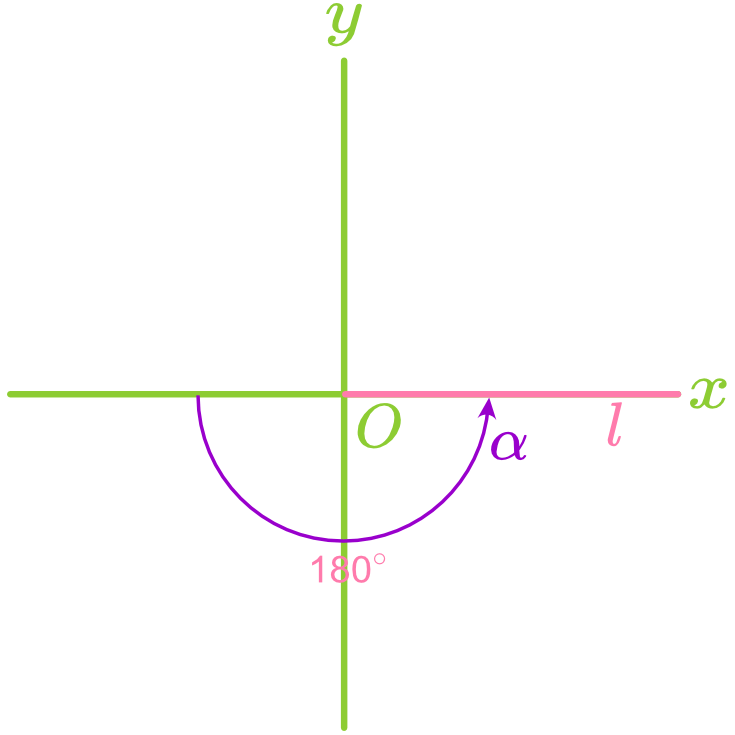
• The angle formed between a straight line and the positive direction of the x-axis is called the angle of inclination, denoted as $\alpha$, where $\alpha \in [0,\pi )$.
  

• Note: When a line is horizontal, its angle of inclination is $0^{\circ }$. When a line is vertical, its angle of inclination is ${90}^{\circ }$.

  • Counterclockwise rotation increases $\alpha$.
  • Clockwise rotation decreases $\alpha$.
  

Jump to heading🔗 2.Definition of Slope

• The tangent of the inclination angle is the slope, denoted as $k=tan\alpha ,\alpha =\frac{\pi }{2}$.

  • $\alpha \mathbf{=}\frac{\mathbf{\text{opposite}}}{\mathbf{\text{adjacent}}}$
    

• Remarks:

  • When $\alpha =0,k=0$; Zero numerator
  • When $0<\alpha <{90}^{\circ },k>0$;
  • When $\alpha ={90}^{\circ }$, $k$ is undefined; Zero denominator
  • When ${90}^{\circ }<\alpha <{180}^{\circ },k<0$;

Jump to heading🔗 3.Common Inclination Angles and Slope

• Supplementary angles: their tangents are opposite numbers.
  • $tan({180}^{\circ }-\theta )=-tan\theta$.

Jump to heading🔗 4.Two-Point Slope Formula

• Let there be two points $P_1(x_1,y_1)$ and $P_2(x_2,y_2)$ in a straight line $l$, then $k=\frac{y_2-y_1}{x_2-x_1},{\mathbf{x}}_{\mathbf{1}}\ne {\mathbf{x}}_{\mathbf{2}}$.

• Special cases:

  • If $y_2=y_1$, the line is horizontal, and $k=0$.
  • If $x_2=x_1$, the line is vertical, and $k=\mathrm{\infty }\vee$undefined.

  • Jump to heading🔗 The slope between $(x,y)$ and $(0,0)$ is $k=\frac{y}{x}$.

Jump to heading🔗 5.Focus 1

Inclination angle and slope

• Pay attention to special inclination angels, such as ${90}^{\circ }$, and observe the sign and magnitude changes of the slope.

Jump to heading🔗 Solution

Jump to heading🔗 Conclusion

• Derived Solution

  $\mathbf{(}\mathbf{B}\mathbf{)}$
  According to the Solution, get $(\text{3})$, so choose $B$.

• Formula used

  $\begin{array}{ll}\{\begin{array}{l}0<\alpha <{90}^{\circ },k>0\\ {90}^{\circ }<\alpha <{180}^{\circ },k<0\end{array}& \text{Definition of slope}\\ {135}^{\circ }=-1& \text{Inclination angle–slope reference}\end{array}$

Jump to heading🔗 Solution

Jump to heading🔗 Conclusion

• Derived Solution

  $\mathbf{(}\mathbf{B}\mathbf{)}$
  According to the Solution, get $k=-\frac{1}{3}$, so choose $B$.

• Formula used

  $\begin{array}{ll}k=\frac{y_2-y_1}{x_2-x_1}& \text{Two-point slope formula}\\ (\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})& \text{Midpoint coordinates}\end{array}$

Jump to heading🔗 6. Equation of a Line

Jump to heading🔗 $\boxed{\text{1}}$Slope-intercept form

• If the slope $k$ and the $\stackrel{\text{y-axis intersection}}{\overbrace{\text{y-intercept }b}}$ are known, the equation of the line can be expressed as $y=kx+b$.
• Special cases:

  • Jump to heading🔗 $b=0:y=kx$ (Passing through the origin)

  • $k=0:y=b$ (Horizontal line)

$\text{Slope-intercept demo}$

Jump to heading🔗 $\boxed{\text{2}}$Point-slope form

• If the slope $k$ and a point $(x_0,y_0)$ are known, the equation of the line can be expressed as $y=y_0+k(x-x_0)$ or $\frac{y-y_0}{x-x_0}=k$.
• Special case: $(x_0,y_0)⟶(0,b)$ The point-slope form becomes the slope-intercept form.
• Equation derivations

  $\begin{array}{l}y=k(x-x_0)+y_0\\ \frac{y-y_0}{x-x_0}=k& \text{Two-point slope formula}\\ y=y_0+k(x-x_0)\end{array}$

$\text{Point-slope demo}$

Jump to heading🔗 $\boxed{\text{3}}$Intercept form

If the x-axis and y-axis intercepts are known to be $a$ and $b$ respectively, the equation of the line can be expressed as $\frac{x}{a}+\frac{y}{b}=1,\mathbf{(}\mathbf{a}\mathbf{,}\mathbf{b}\ne \mathbf{0}\mathbf{)}$.

Jump to heading🔗 $\boxed{\text{4}}$Two-point form

If the coordinates of two points $(x_1,y_1)$ and $x_2,y_2$ are known, the equation of the line can be expressed as $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$.

• Special case:
  • The intercept form is a special case of the two-point form.
  • The two-point form can be changed into the point-slope form.
• Equation derivations

  $\begin{array}{ll}\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}& \text{Similarity ratio}\\ y-y_1=\frac{x-x_1}{x_2-x_1}(y_2-y_1)\\ y-y_1=\underset{k}{\underbrace{\boxed{{\displaystyle \frac{y_2-y_1}{x_2-x_1}}}}}(x-x_1)& \text{Point-slope form}\end{array}$

Jump to heading🔗 $\boxed{\text{5}}$General form

• The above equations can all be transformed into a linear function $ax+by+c=0$, which is called the general form of the equation of a line.

• Jump to heading🔗 Remark: The general form is very important, as it allows you to quickly calculate the slope $k=-\frac{a}{b}$.

  • $k=-\frac{a}{b}$ derivations

    $\begin{array}{l}ax+by+c=0⟶by=-ax-c\\ y=\underset{k}{\underbrace{-\boxed{{\displaystyle \frac{a}{b}}}}}x-\frac{c}{b}\\ \text{Example:}\\ 4x+3y-5=0\to k=-\frac{4}{3}\end{array}$

• Jump to heading🔗 Quickly calculate the Intercept form

  $\begin{array}{l}y=0\{\begin{array}{l}\begin{array}{l}ax+b0+c=0\\ ax+c=0\\ ax=-c\\ x=-\frac{c}{a}\end{array}\end{array}\\ x=0\{\begin{array}{l}\begin{array}{l}a0+by+c=0\\ by+c=0\\ by=-c\\ y=-\frac{c}{b}\end{array}\end{array}\\ \text{Calculate the area of the triangle formed by the intercept form:}\\ S=\frac{1}{2}ah\\ S=\frac{1}{2}\times -\frac{c}{a}\times -\frac{c}{b}\\ S=\frac{c^2}{2|ab|}\end{array}$

• Special case:

  • Jump to heading🔗 $a=0:by+c=0$ (Horizontal line)

  • $b=0:ax+c=0$ (Vertical line)
  • $c=0:ax+by=0$ (Line passing through the origin)

Jump to heading🔗 7.Focus 2

Equation of a line

• Master the various forms of the equation of a line and their applicable situations, and understand the differences between the different forms of the equation.

Jump to heading🔗 Solution

Jump to heading🔗 Conclusion

• Derived Solution

  $\mathbf{(}\mathbf{C}\mathbf{)}$
  According to the Solution, get $(\text{2}),(\text{4})$, so choose $C$.

• Formula used

  $\begin{array}{ll}\frac{x}{a}+\frac{y}{b}=1& \text{Intercept form}\\ y=y_0+k(x-x_0)& \text{Point-slope form}\\ ax+by+c=0& \text{General form of a line}\end{array}$

• Line representation of the equation of a straight line

  
  

  Equations	Horizontal Line	Vertical Line	Line Passing Through the Origin	Other Lines
  Slope-intercept form	✅	❌	✅	✅
  Point-slope form	✅	❌	✅	✅
  Intercept form	❌	❌	❌	✅
  Two-point form	❌	❌	✅	✅
  General form	✅	✅	✅	✅

Jump to heading🔗 Solution

Jump to heading🔗 Conclusion

• Derived Solution

  $\mathbf{(}\mathbf{D}\mathbf{)}$
  According to the Solution, get $x=\frac{1}{2}$, so choose $D$.

• Formula used

  $\begin{array}{ll}k=\frac{y_2-y_1}{x_2-x_1}& \text{Two-point slope formula}\end{array}$

Jump to heading🔗 Solution

Jump to heading🔗 Conclusion

• Derived Solution

  $\mathbf{(}\mathbf{E}\mathbf{)}$
  According to the Solution, get $x-y+3=0\vee 8x-5y=0$, so choose $E$.

• Formula used

  $\begin{array}{ll}\frac{x}{a}+\frac{y}{b}=1& \text{Intercept form}\\ y=kx& \text{Passing through the origin}\\ k=\frac{y}{x}& \text{Slope of the line passing through the origin}\end{array}$

• Opposite intercepts and equal Intercepts

  • The intercepts are opposites.
    
    ① $k=1$.
    ② Passes through the origin.
  • The intercepts are equal.
    
    ① $k=-1$.
    ② Passes through the origin.

Jump to heading🔗 Solution

Jump to heading🔗 Conclusion

• Derived Solution

  $\mathbf{(}\mathbf{E}\mathbf{)}$
  According to the Solution, get $b=-5$, so choose $E$.

• Formula used

  $\begin{array}{ll}k=\frac{y_2-y_1}{x_2-x_1}& \text{Two-point slope formula}\\ \frac{x}{a}+\frac{y}{b}=1& \text{Intercept form}\\ y=y_0+k(x-x_0)& \text{Point-slope form}\\ y=kx+b& \text{Slope-intercept form}\end{array}$

Jump to heading🔗 Solution

Jump to heading🔗 Conclusion

• Derived Solution

  $\mathbf{(}\mathbf{B}\mathbf{)}$
  According to the Solution, get $4\times (-6)=-24$, so choose $B$.

• Formula used

  $\begin{array}{ll}ax+by+c=0& \text{General form of a line}\\ \{\begin{array}{l}\text{y-intercept}=-\frac{c}{b}\\ \text{x-intercept}=-\frac{c}{a}\end{array}& \text{Quickly convert the general form to the intercept form}\end{array}$

• Additionally, If the problem is to calculate the area of the triangle formed by the intercept form

  
  $\begin{array}{l}2x-3y+12=0\\ S=\frac{c^2}{2|ab|}\\ S=\frac{{12}^2}{2|2\times -3|}=\frac{24}{12}=12\end{array}$

Jump to heading🔗 8.Focus 3

The line passes through quadrants

• Analyze the graph based on the slope and intercepts of the line.
• Remember the conclusion: When $k>0$, the line must pass through the first and third quadrants; when $k<0$, the line must pass through the second and fourth quadrants.
  

Jump to heading🔗 Solution

Jump to heading🔗 Conclusion

• Derived Solution

  $\mathbf{(}\mathbf{A}\mathbf{)}$
  According to the Solution, get $(\text{1})✅,(\text{2})❌$, so choose $A$.

• Formula used

  $\begin{array}{ll}\{\begin{array}{l}\text{y-intercept}=-\frac{c}{b}\\ \text{x-intercept}=-\frac{c}{a}\end{array}& \text{Quickly convert the general form to the intercept form}\\ a=0⟶by+c=0& \text{Horizontal line}\\ k=-\frac{a}{b}& \text{Quickly convert the general form to the slope}\\ {90}^{\circ }<\alpha <{180}^{\circ },k<0& \text{Definition of slope}\end{array}$